Since last week I’ve finally relocated to Gothenburg! Together with a class mate, I will write my master thesis on a consultant company called Knowit. The thesis will be about crypto in cloud services with focus on a swedish law called offentlighets- och sekretesslagen.

I hope to get some more frequent updates on the blog in the coming months. But today I wanted to show a basic crypto attack, the bitflip attack on AES_CBC.

What is AES_CBC?

The “normal” mode of operation for AES is AES ECB(Electronic Codebook). This has some problems. Most importantly, a plaintext is always represented as the same ciphertext block when encrypted under the same key. This can lead to some fun statistical attacks :)

To solve this we can introduce a random vector into the encryption routine. This leads us straight into AES_CBC!

AES_CBC works by introducing a random initialization vector(IV) and chaining the blocks so that each block is “dependant” on the previous block.

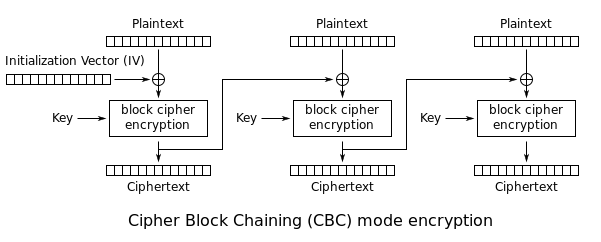
Bitflip???

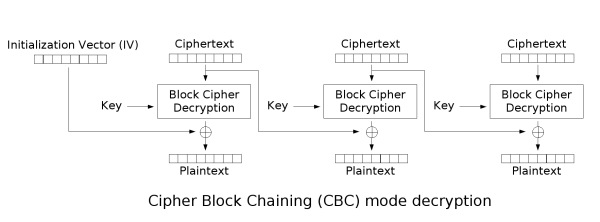
The basic idea is that since each plaintext block is XORed with the previous ciphertext block we can alter(flip) the ciphertext to represent the plaintext we want it to be (if we know/can guess the original plaintext). Let’s look at the decryption routine!

Imagine we have a ciphertext that looks like (block size=4)

ABCDEFGH

with the plaintext

BITFLIP!

Our goal is to flip the 5th character in the plaintext (L) to K.

Look at how CBC works. The previous ciphertext block is XORed with the decrypted ciphertext block to represent the plaintext block. Maybe a bit confusing, but it’s actually simple.

L = A^decrypt(EFGH)[0]

Now, lets do the attack. We want L to be represented as K.

CIPHERTEXT = ABCDEFGH
TARGET = BITFKIP!

CIPHERTEXT[0] = A^L^K
FLIPPED = decrypt(CIPHERTEXT)

FLIPPED == TARGET?
true

Why does this work?

Think about how XOR works

L = A^decrypt(EFGH)[0]

What do we control here? The ciphertext. So what does the ciphertext have to be in order for L to become K in the plaintext?

Remember that

decrypt(EFGH)[0] = A^L

What do we need to put in Y for

K = Y^decrypt(EFGH)[0]

to be true?

Y = A^L^K (since decrypt(EFGH)[0] = A^L)

Code example

Now imagine we encrypt session tokens or cookies with AES_CBC…

import json
from base64 import b64encode, b64decode
from Crypto.Cipher import AES
from Crypto.Random import get_random_bytes
from Crypto.Util.Padding import pad, unpad


class AES_CBC():
    
    def __init__(self, blksize=16):
        if blksize not in [16, 24, 32]:
            raise ValueError("Blocksize must be 16, 24 or 32")

        self.blksize = blksize
        self.key = get_random_bytes(self.blksize)

    def encrypt(self, plaintext):
        cipher = AES.new(self.key, AES.MODE_CBC)
        pt_padded = pad(plaintext, AES.block_size)
        ct_bytes = cipher.encrypt(pt_padded)
        iv = b64encode(cipher.iv).decode('utf-8')
        ct = b64encode(ct_bytes).decode('utf-8')
        
        return json.dumps({
            'IV':iv,
            'ciphertext':ct
        })

    def decrypt(self, cipher_obj):
        b64 = json.loads(cipher_obj)
        iv = b64decode(b64['IV'])
        ct = b64decode(b64['ciphertext'])
        cipher = AES.new(self.key, AES.MODE_CBC, iv) 
        pt_padded = cipher.decrypt(ct)
        
        return unpad(pt_padded, AES.block_size)
    

if __name__ == "__main__":
    aes = AES_CBC()
    res = aes.encrypt(b"{id=11;date=20200129;role=common}")
    
    b64 = json.loads(res)
    ct = b64decode(b64['ciphertext'])
    iv = b64['IV']
    
    to_flip = list(ct)
    target = "admin;"
    before = "common"
    for i in range(6):
        to_flip[10+i] = ct[10+i]^ord(before[i])^ord(target[i])
    
    flipped = json.dumps({
        'IV':iv,
        'ciphertext': b64encode(bytes(to_flip)).decode('utf-8')
    })

    print(aes.decrypt(flipped))

How do I mitigate this??

Change to a more modern mode of operation. Or do MAC then Encrypt!