Breaking AES GCM Part 1
This is a small three-part series where I will show some attacks and implementation of AES GCM, and why GCM is a good idea. Let’s get started!
Why does AES GCM exist?
So it seems like AES is a bit complicated. Most people see AES and think - “Great! This can’t be broken”.
And sure, it isn’t feasible in any amount of time to get the key from a ciphertext, even when knowing the plaintext. But there are other problems with the implemenation of AES. Let’s look at the most basic mode of operation, AES ECB.
ECB
ECB, or Electronic Codebook is the simplest mode of operation. You divide the plaintext into blocks and encrypt the blocks separately.
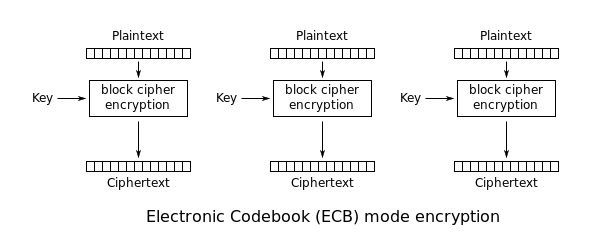
What’s the problem with this? Two encrypted plaintexts will always be represented as the same ciphertext (if encrypted with the same key, of course).
CBC
Ok, ECB is bad. But what if we add another random element into the encryption of each block, so two encrypted plaintexts will not be represented as the same ciphertext. This seems like a good idea! Let’s do it.
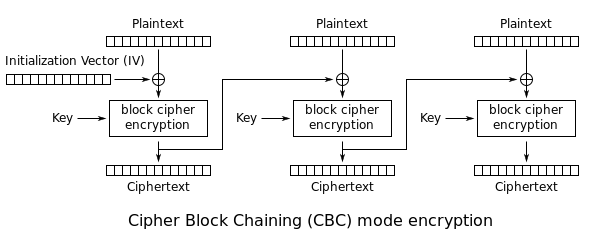
CBC stands for Cipher Block Chaining, as the encryption of each block is dependant on the ciphertext from the previous block. This looks much better! But with this chaining comes other problems, like bitflipping attacks.
I’ve written some code on a basic bitflipping attack here. The basic idea of a bitflipping attack is that if the attacker know the plaintext, he/she can do some math to change the ciphertext into being decrypted into anything. Oh, that’s bad.
CTR
CTR stands for Counter. Instead of splitting the plaintext into blocks and padding it, we can have a counter with a random nonce (like IV) and XOR the “keystream” with the plaintext. This turns the AES block cipher into a stream cipher, which is a more logic way of looking at data. This is also suspectible to bitflipping attacks. attack code.
How do we fix this? By adding integrity checks of course! Which leads us perfectly into AES GCM.
GCM
GCM stands for Galois Counter Mode. This is bit more complex solution, since adding a simple hash after the ciphertext would fix nothing (since the attacker can modify the hash to the flipped code). GCM implements a type of MAC. This makes it near impossible for an attacker to fiddle with the ciphertext, since any change would be detected when comparing the hashes. And the attacker can’t spoof the hash, since he/she doesn’t know the secret.
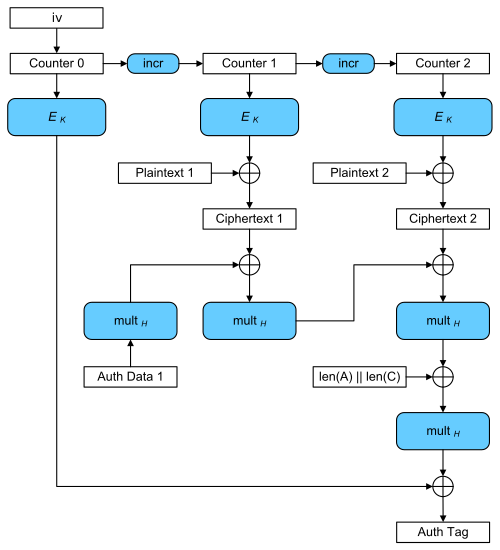
Some explanation:
- Auth Data 1: The Additional data which you can put into the GHASH function. GCM is an AEAD (Authenticated Encryption Additional Data) algorithm.
- mult_H:. “Each round” of the GHASH function. The input data is multiplied with Ek(0^128) in a Galois Field (GF(2^128)).
Galois field as a MAC is chosen because it actually allows the Auth Tag calculation to be computed in parallel, which makes it faster than for example CBC. And even more so, than a traditional SHA-1 MAC. And speed in cryptography is important.